大家好,今天给大家介绍标准差。标准差在统计领域是一个重要概念,有些地方晦涩难懂,特别是样本标准差的分母为何是n-1,而不是n或n-2,接下来我会一一介绍并用计算机模拟难点。
什么是标准差?下面看两组数[28,29,30,31,32],[10,20,30,40,50],它们的平均数都是30。这两组数是一致的吗?实际上,这两组数离散程度有很大区别。

用numpy模块计算,两组数的标准差相差10倍

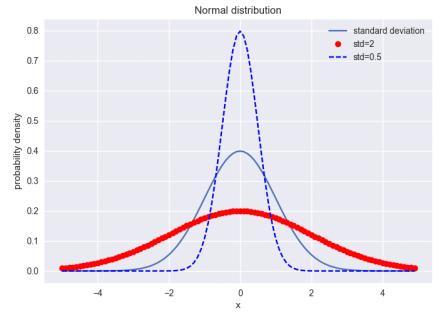
方差是实际值与期望值之差平方的平均值。方差,通俗点讲,就是和中心偏离的程度!用来衡量一批数据的波动大小(即这批数据偏离平均数的大小)并把它叫做这组数据的方差。记作S2。 在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定。标准差就是方差的平方根。方差和标准差用于不同场合,方便计算。
(标准差英文解释)

方差公式
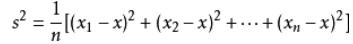
标准差公式
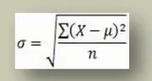
难点来了,总体标准差和样本标准差的公式是有区别的,如下图

样本标准差公式中,分母是n-1。
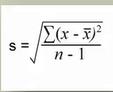
为何样本标准差的分母为何是n-1,而不是n或n-2?
我们用计算机建模,环境Anaconda(python2.7)

参数解释:
Sigma表示总体标准差
S表示样本标准差
ddofValue=0 表示样本标准差分母是n
ddofValue=1 表示样本标准差分母是n-1
ddofValue=2 表示样本标准差分母是n-2
算法思路:
1.模拟出一个总体(服从正态分布的1000个随机数)
2. 从总体中随机抽样(100个随机数)
3.分别算出总体和样本的标准差,然后相减得到distance差值
4.循环1000次试验,把1000个distance相加,得到total_distance
5.在步骤3中,分别对样本标准差的分母取n, n-1,n-2, 最终得到dict_modes
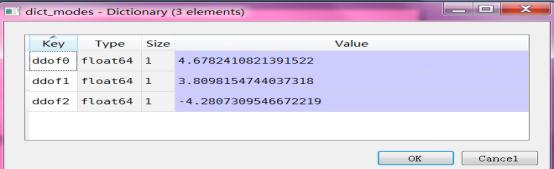
观察dict_modes,ddof1的绝对值最小3.8
ddof1=1 表示样本标准差分母是n-1
总结:s样本标准差的分母采用n-1更加接近真实的总体标准差。通过计算机模拟,我们证明了为什么样本标准差的分母n-1比较合适,而不是n或n-2。
源代码:
如果允许代码有任何问题,请反馈至邮箱231469242@qq.com
# -*- coding: utf-8 -*-
'''
为什么样本标准差的分母是n-1
'''
import random
import numpy as np
#试验次数
trial=1000
#正态分布总体大小
size_total=1000
#正态分布样本大小
size_sample=100
#分母状态
#ddofValue=0 表示样本标准差分母是n
#ddofValue=1 表示样本标准差分母是n-1
#ddofValue=2 表示样本标准差分母是n-2
list_ddofValues=[0,1,2]
#返回样本标准差和总体标准差的距离总和
def Total_distance(ddofValue):
#总体标准差 和样本标准差的差值
total_distance=0
for i in range(trial):
normal_values=list(np.random.normal(size=size_total))
#总体标准差
sigma=np.std(normal_values,ddof=0)
#随机抽样
sample=random.sample(normal_values,size_sample)
s=np.std(sample,ddof=ddofValue)
distance=sigma-s
total_distance+=distance
return total_distance
#选择最佳模型
def Dict_modes():
distance_ddof0=Total_distance(list_ddofValues[0])
distance_ddof1=Total_distance(list_ddofValues[1])
distance_ddof2=Total_distance(list_ddofValues[2])
dict_modes={}
dict_modes["ddof0"]=distance_ddof0
dict_modes["ddof1"]=distance_ddof1
dict_modes["ddof2"]=distance_ddof2
return dict_modes
dict_modes=Dict_modes()
print dict_modes
'''
for i in range(trial):
normal_values=list(np.random.normal(size=n))
#总体标准差
sigma=np.std(normal_values,ddof=0)
#plt.hist(normal_values)
#随机抽样
sample=random.sample(normal_values,100)
#plt.hist(sample)
s=np.std(sample,ddof=ddofValue)
distance=sigma-s
total_distance+=distance
print"when ddofValue is:",ddofValue
print"Distance:",total_distance
来源:莫然博客,欢迎分享本文!